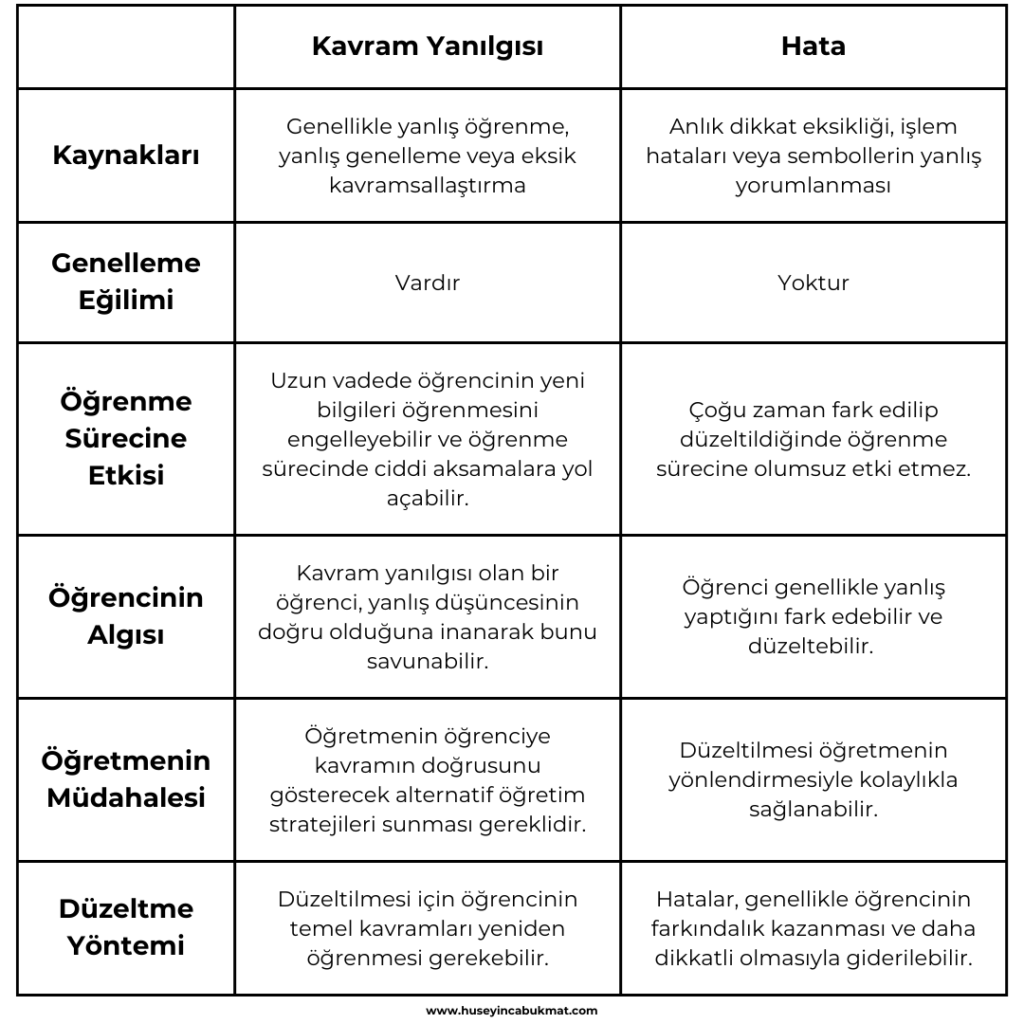
Kavram Yanılgısı Ve Hata
Matematiksel hatalar öğrencilerin yeni problemlerle karşılaşıp, üretimleri yanlış genellemeleri sonucu ortaya çıkar. Örneğin, öğrenciler çıkarma işleminde, onluk bozmadan her sütunda büyük sayıdan küçük sayıyı çıkarırlar. Bu yöntemin onluk bozma içeren diğer problemlere de genellenmesi çok kolaydır. Öğrenciler problemi çözemediklerinde, bırakmak yerine kuralları probleme uyacak şekilde değiştirir. Hatalı çözüm yolları kalıcı olabilir ve yanlış bir özyeterlilik algısı yaratabilir. Bu algının sebebi, öğrencinin işlemden bir sonuç elde etmemesi olabilir. (Schunk, 2011; s.432).
Hatalar genellikle öğrenme için ‘doğru’ cevaplardan daha bilgilendiricidir. Bir öğrencinin matematiksel bir kavramı ne kadar iyi kavradığını değerlendirmek hem de öğrencinin fikirlerini geliştirmek ve uyandırmak için geribildirim verme konusunda fırsatlar sunar. Başarılı öğrenciler bile basit konular gibi görünen yeni konularda zorluk yaşayabilir (Hodgen ve Askew, 2010; s.141).
Hata analizi iki açıdan önem kazanmaktadır. Bunlardan ilki akademik uygulamaların gerekliliklerine göre öğrenme zorluklarını teşhis etmek, bireysel olarak öğrencilerin farkındalıklarını, performans ve anlayışlarını arttırmak için matematik eğitiminde farklı yöntemlerin geliştirilmesini sağlar. İkinci olarak da hata analizi matematik öğretme-öğrenim süreci üzerinde dikkat çekici bir başlangıç noktası olarak görülmektedir. Hata analizi matematik öğrenmenin bazı temel sorunlarını açığa kavuşturmak için umut verici bir araştırma stratejisi olarak düşünülmektedir (Radatz, 1980).
Bir çocuğun matematiksel bir hatayı yaptığı zaman dikkate alınması gereken en belirgin olasılıklar şunlardır (Cockburn, 2005; s.6).
- Hangi işlemin uygulanacağını biliyor mu? (Örneğin; çocuk + sembolünün ‘ekleme’ anlamına geldiğini biliyor mu, yoksa yerine çıkarma veya bölme işlemini mi yapıyor.)
- İşlemin doğru şekilde nasıl yapılacağını biliyor mu? (Örneğin; çocuk ayrıştırılması gereken miktarlarda gerekli dönüşümü yapabilir mi?)
- Yapılacak işlem sürecini hem kullanılan dil hem de matematiksel açıdan anlıyor mu?
Temel gerçekler ve dikkatsizlik sonucu kaynaklanan hatalar hariç olmak üzere, öğrencilerin yaptıkları hatalar rastgele değildir. Yapılan hatalar son derece tutarlıdır. Öğretmenler yıllarca aynı hataları tekrar tekrar görürler. Çoğu durumda, çocukların hataları kurallara bağlı, doğru bir algoritma yerine yanlış bir işlemin uygulanmasının sonucudur. Ancak bu yanlış işlemler de mantık yanlış olsa dahi, çocuğa mantıklı gelebilir (Burns, 2007; s.10).
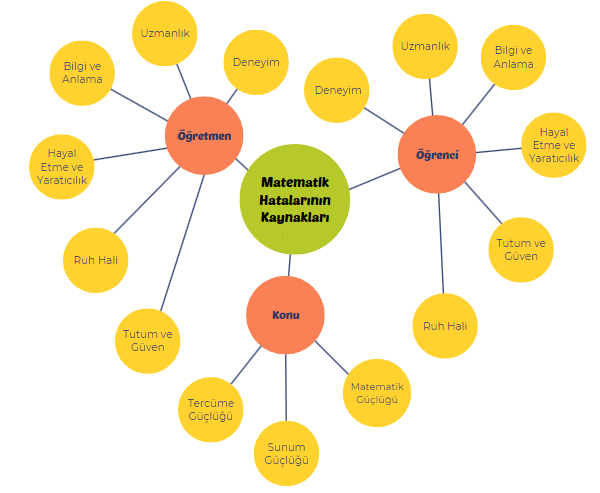
Hatalar kavram yanılgılarının yanı sıra dikkatsizlik, anlık bir kalem kayması, sembollerin ve metinlerin yanlış yorumlanması, matematiksel konu, öğrenilen hedef ve kavram hakkında deneyim, anlama ve bilgi eksikliği, verilen cevabı kontrol etmede farkındalık eksikliği, yetersizlik gibi birçok nedenden de kaynaklanabilmektedir (Cockburn, 2005; Burns, 2007; Ryan ve Williams, 2007; Hansen, 2014).
İçindekiler
ToggleKavram Yanılgısı Veya Hata Nasıl Ayırt Edilir?
Öğrencilerin matematiksel kavramlara ilişkin yaptıkları hataları belirlemek ve oluşumlarını engellemek oldukça önemlidir. Matematik yığılmalı bir disiplin olduğundan dolayı öğrenilen her bir kavram bir sonraki kavramın öğrenilmesini etkilemektedir. Herhangi bir kavramın öğrenilmesinde yaşanan güçlük ya da yanlış öğrenmeler sonraki birçok kavramın yanlış algılanmasına ve güçlükler yaşanmasına neden olabilir (Zembat, 2010; s.10).
Tamamlanmış bir çalışmaya baktığımızda kavram yanılgısına veya başka bir nedenden kaynaklanan bir hata olduğunu anlamımızın en iyi ipucu hatanın sıklığı ve tutarlılığıdır (Spooner, 2002; s.3).