Asal Sayılar Neden Sonsuzdur?

Asal sayılar, matematiğin en ilginç temel taşlarından biridir. Kendilerinden ve 1’den başka böleni olmayan bu özel sayılar, sayılar teorisinin en büyük kahramanları arasında yer alır. 2, 3, 5, 7, 11… diye giderler ama bir soru var ki hepimizin aklını kurcalar: “Asal sayılar sonsuz mudur?”

Bu soruya ilk kesin cevabı veren kişi Antik Yunan’ın ünlü matematikçisi Öklid’dir. Yaklaşık 2300 yıl önce yazdığı Elementler adlı eserinde asal sayıların sonsuz olduğunu kanıtlamıştır. Üstelik bu ispat mantığın en güçlü tekniklerinden biri olan “olmayana ergi” (çelişki yöntemi) ile yapılmıştır. Gelin bu kanıtı beraber inceleyelim:
Varsayalım ki asal sayılar sonlu sayıda olsun. En büyük asal sayımız da x olsun.
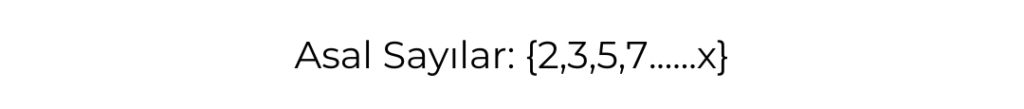
Asal Sayılar kümesindeki bütün elemanları çarpalım ve üzerine bir ekleyelim. Bu sayının A sayısına eşit olduğunu yazalım.
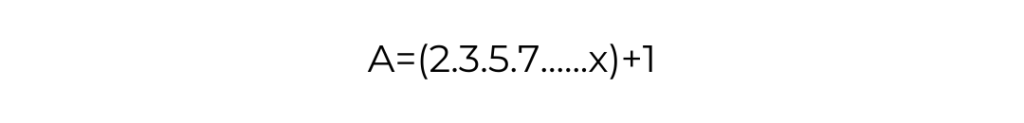
Buraya kadar geldikten sonra Aritmetiğin Temel Teoremi‘ne başvururuz.
Aritmetiğin temel teoremi, birden büyük her doğal sayının asal sayıların çarpımı şeklinde, üstel olarak ve yalnızca bir şekilde yazılabileceğini ifade eder. Yani her doğal sayı, asal çarpanlarına ayrıldığında bu çarpanlar sırasız olarak benzersizdir.
O halde elde ettiğim A sayısını belli sayıların çarpımı olarak yazabilmeliyim. Fakat baktığımda A sayısını bölebilecek herhangi bir asal bulamam. Çünkü 2’den x’e kadar olan bütün asal sayıların çarpımının bir fazlası A sayısıdır. A sayısını bölen bir asal sayı yoktur. 1 olmasa A sayısı kalansız bölünebilecekken 1’den dolayı hiçbir asal sayı A sayısını tam olarak bölememektedir.
Böylelikle iki seçeneğimiz oluşur:
- Aritmetiğin temel teoremi yanlıştır. Çünkü elde ettiğimiz A sayısı aritmetiğin temel teoremine göre kesinlikle bir asala bölünmeli. Ama bizim elimizdeki asal sayıların hiçbirine bölünmemektedir. Aritmetiğin temel teoreminin mutlaka doğru olduğunu bildiğimizden dolayı “x’ten daha büyük asal sayılar var ve A sayısı bu asal sayılara bölünmektedir.” çıkarımını yapabiliriz. A sayısı mutlaka bir asal sayıya bölünmelidir. Fakat x’den daha büyük bir asal sayı varsa en büyük asal sayıdan daha büyük bir asal sayı var demektir. Bu ise bir çelişkidir.
- A sayısı asal sayıdır. Çünkü A sayısı hiçbir asal sayıya bölünemedi. Fakat biz ispatımıza başlarken x sayısının en büyük asal sayı olduğunu kabul etmiştik. Asal sayıların tamamının çarpımı ile A sayımızı elde ettiğimize göre A sayısı x sayısından büyüktür. Bu da bir çelişkidir.
İki durumda da çelişkiyle karşılaştığımıza göre ispatımızın en başında yaptığımız varsayım yanlıştır. Asal sayılar sonlu değil sonsuzdur.

Bu ispat matematik dünyasında büyük bir dönüm noktasıdır. Çünkü asal sayılar sayılar teorisinin temel taşlarından biridir. Matematiğin nasıl sağlam bir mantık üzerine kurulduğunu da gösterir.
Modern kriptografi asal sayıların bu özel yapısından faydalanarak güvenlik sistemleri kurar. Şifreleme ve güvenlik sistemleri için asal sayıların yeri tartışılamaz.
Ayrıca asal sayılar, sayıların temel yapı taşları olduğu için tüm doğal sayıların çarpanlarına ayrılmasında kritik bir rol oynar.
Peki şu ana kadar bulunan en büyük asal sayı nedir? Meraklıları için söyleyelim. Şu an bilinen en büyük asal sayı:
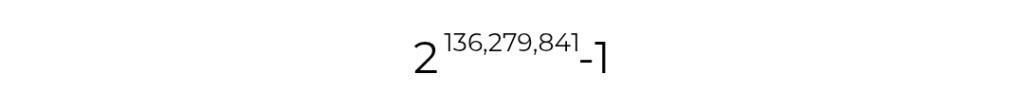
Tam 41,024,320 basamak uzunluğundadır. Basamak sayısının bile okunması zor. Bu tarz devasa asal sayılar Mersenne Asalları olarak bilinir. Günümüzde bilgisayarlar tarafından keşfedilmeye devam ediyor.
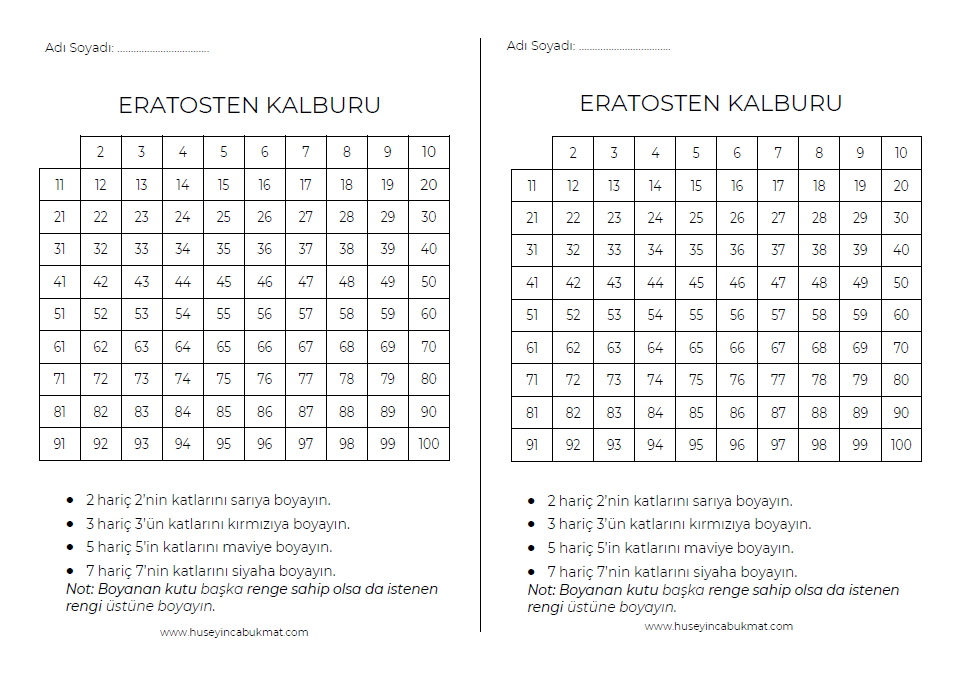
Asal sayılarla ilgili bir diğer önemli kavram da Eratosthenes Kalburu. Bir sayı listesinden asal olmayanları eleyerek asal sayıları bulmaya yarayan oldukça etkili bir yöntemdir. Günümüzde bile bilgisayarlar, büyük asal sayıları tararken bu basit ama güçlü yöntemi kullanıyor.
Öklid’in binlerce yıl önce yaptığı bu ispat günümüzde hala matematiğin en güzel ve zarif kanıtlarından biri olarak kabul ediliyor. Sonsuz sayıda asal sayı olması matematiğin ne kadar derin ve keşfedilmeyi bekleyen sırlarla dolu olduğunu bir kez daha gösteriyor.



