Matematiğin Seyrini Değiştiren Kitaplar: Formüllerin Ötesindeki Miras
Matematik denince akla çoğu zaman formüller, semboller ve soyut ispatlar gelir. Oysa tarihin her döneminde, birkaç satırlık bir metin ya da tek bir kitap, bilimin tüm yönünü değiştirecek kadar güçlü olmuştur. Bu kitaplar yalnızca yeni fikirler sunmamış, insanın düşünme biçimini de kökten dönüştürmüştür. Her biri, hem dönemin eğitim anlayışına hem de matematiğin doğasına yön vermiştir.
İçindekiler
ToggleÖklid: Düşüncenin Mimarisi

Yaklaşık MÖ 300 yılında kaleme alınan Elementler, matematik tarihinin en etkili eserlerinden biridir. Öklid, kendisinden önceki dağınık bilgileri toplayarak onları birkaç temel önermeden yola çıkan bir yapı haline getirdi. Bu, aksiyomatik yöntemin doğuşuydu. Artık bir önermenin doğruluğu gözleme değil, mantığa dayanıyordu. Öklid’in bu yaklaşımı yalnızca geometriyi değil, tüm bilimlerin yöntemini etkiledi. Eğitimde bugün kullandığımız “ispat kültürü” onun mirasıdır.
Arşimet: Keşfin ve Mantığın Dengesi

Öklid düşüncenin düzenini kurduysa, Arşimet keşfin cesaretini temsil eder. Küre ve Silindir Üzerine ve özellikle kayıp eseri Yöntem, modern kalkülüsün ilk adımlarıydı. Arşimet, bir kürenin hacmini hesaplamak için cismi sonsuz ince dilimlere ayırıp mekanik prensiplerle dengeledi. Bu yöntem, bugünkü integral hesabının sezgisel atasıdır. Onun sezgisel keşifleri, matematiğin yalnızca sonuçlardan değil, düşünme süreçlerinden oluştuğunu gösterir.
Diophantus: Sayının Dili

MS 3. yüzyılda yazılan Arithmetica, cebirsel düşüncenin ilk olgun örneğidir. Diophantus, sayılarla ilgili problemleri semboller aracılığıyla ifade ederek “senkoplu cebir” dediğimiz ara bir dil geliştirdi. Bu adım, matematiğin soyut diline geçişin başlangıcıydı. Yüzyıllar sonra Fermat’nın aynı kitabın kenarına düştüğü küçük bir not, modern sayı teorisinin doğmasına yol açtı. Böylece Arithmetica, yalnızca geçmişin değil, geleceğin de kitabı oldu.
Brahmagupta: Sıfırın Keşfi

Hintli matematikçi Brahmagupta, 628 yılında yazdığı Brahmasphutasiddhanta adlı eserinde sıfır ve negatif sayılarla işlem kurallarını tanımladı. Bu, insan zihninin soyutlamadaki en büyük sıçramalarından biriydi. “Sıfır” artık yokluğu değil, sistemin bir parçasını temsil ediyordu. Matematiksel düşünme, somuttan soyuta geçişin eşiğini bu kitapla aştı.
Hârizmî: Algoritmanın Doğuşu

Brahmagupta’nın temellerini sistemleştiren Hârizmî, El-Kitabü’l-Muhtasar fi Hisab el-Cebr ve’l-Mukabele adlı kitabıyla cebiri bağımsız bir disiplin haline getirdi. Onun kullandığı “el-cebr” terimi, bugün “algebra” olarak yaşıyor. Hârizmî, denklemleri çözmek için adım adım ilerleyen bir yöntem geliştirdi ve bu sistematik düşünme biçimi “algoritma” kavramının doğmasına yol açtı. Eğitim açısından bu kitap, problem çözmeyi ezberden çıkarıp, düşünsel bir süreç haline getiren ilk eserdi.
Fibonacci: Sayıların Avrupa’ya Yolculuğu

1202’de yayımlanan Liber Abaci, Hârizmî’nin fikirlerini Avrupa’ya taşıdı. Fibonacci, Hindu-Arap sayı sistemini tanıtarak Roma rakamlarının sınırlılığını ortadan kaldırdı. Sıfır ve basamak değerinin tanıtılması, Avrupa’da hesaplamayı bir devrime dönüştürdü. Bu kitap, ticaretten bilime kadar her alanda yeni bir çağ başlattı. Bugün öğrencilerin kullandığı onluk sistem, bu sessiz devrimin mirasıdır.
Kopernik: Evrenin Matematiksel Yüzü

1543 tarihli De Revolutionibus Orbium Coelestium, sadece gökbilim tarihinin değil, matematiksel düşüncenin de dönüm noktasıydı. Kopernik, evrenin merkezine Güneş’i yerleştirerek insanın bakış açısını değiştirdi. Bu değişim, matematiği doğanın dili haline getirdi. Artık bir modelin değeri, gözlemi “kurtarmasıyla” değil, sade ve tutarlı bir matematiksel yapıya sahip olmasıyla ölçülüyordu.
Descartes: Cebir ve Geometrinin Evliliği

1637’de yayımlanan La Géométrie, analitik geometrinin doğuşuydu. Descartes, geometrik şekilleri cebirsel denklemlerle ifade ederek iki alanı tek bir çatı altında birleştirdi. Bugün kullandığımız x ve y harfleriyle tanımlanan koordinat sistemi onun eseridir. Bu fikir, soyut düşüncenin görsel karşılığını yarattı ve matematik eğitiminde temsil gücünü katladı.
Newton: Doğanın Matematiksel Yasaları

1687’de yayımlanan Principia Mathematica, matematik ile fiziği kaynaştırdı. Newton, hareket ve kütleçekim yasalarını formüle ederken kalkülüsü kullandı. Bu kitap, matematiğin evreni açıklama gücünü kanıtladı. Ancak Newton, yöntemlerini klasik geometrinin diliyle sundu; bu, ispatın gücünü korurken İngiliz matematiğini uzun süre geleneksel bir biçimde tutacaktı.
Leibniz: Notasyonun Gücü
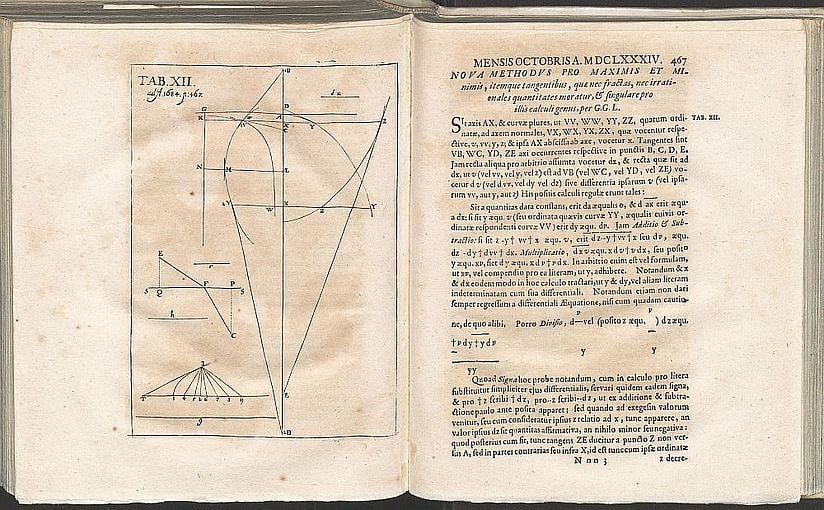
Newton’dan sadece birkaç yıl sonra, Leibniz diferansiyel kalkülüsü yayınladı. Onun kullandığı $dx$ ve $dy$ sembolleri, düşünceyi sadeleştirdi ve işlemleri mekanikleştirdi. Bugün türev ve integral konularında kullandığımız tüm semboller, Leibniz’in bu notasyon devriminden gelir. Matematiği öğretilebilir, paylaşılabilir bir dil haline getiren şey tam da bu sadeliktir.
Euler: Fonksiyonun Krallığı

- yüzyılda Euler, Introductio in analysin infinitorum adlı eseriyle modern analizin dilini oluşturdu. “Fonksiyon” kavramını merkeze aldı. Pi, e, sin, cos gibi sabitleri standartlaştırdı. Euler, soyut düşünceyi bir sistem haline getirdi. Eğitim açısından onun mirası, “matematiksel dilin standardizasyonu”dur. Bugün tüm dünyada aynı sembollerle konuşuyoruz çünkü Euler bu dili yazdı.
Gauss: Sayının Gizli Düzeni

1801’de yayımlanan Disquisitiones Arithmeticae, modern sayı teorisinin temelini attı. Gauss, modüler aritmetiği tanımlayarak sayıların davranışını farklı sistemlerde incelemenin yolunu açtı. Onun kurduğu yapı, cebirsel soyutlamanın ilk adımıydı. Eğitimde, soyutlama ve genelleme kavramlarının kökleri bu kitapta bulunur.
Cauchy: Kesinliğin Dönüşü

1821’deki Cours d’Analyse, analizin titizlikle yeniden yazıldığı bir dönemin başlangıcıdır. Cauchy, limit ve süreklilik kavramlarını kesin tanımlarla ele aldı. Sonsuz küçüklerin sezgisel kullanımı yerini mantıksal temellere bıraktı. Bu yaklaşım, öğrencilerin “neden” sorusunu sormasını sağlayan modern analiz anlayışının temelidir.
Riemann: Asalların Müziği

1859’da yayımlanan kısa ama derin bir makalesinde Riemann, asal sayıların dağılımını karmaşık düzlemdeki bir fonksiyonla ilişkilendirdi. Bu fikir, analitik sayı teorisinin doğuşuydu. Riemann Hipotezi, bugün bile çözülememiş en büyük matematiksel sorudur. Onun düşüncesi, matematiğin farklı alanlarını birleştiren bir köprü haline geldi.
Cantor: Sonsuzluğun Matematiği

- yüzyılın sonlarında Georg Cantor, sonsuzluk kavramını somutlaştırdı. “Küme teorisi” ile sonsuz kümelerin bile farklı büyüklüklere sahip olabileceğini gösterdi. Bu fikir, sezginin sınırlarını zorladı. Matematik eğitimi açısından Cantor’un katkısı, öğrenciyi düşünsel rahatlık alanının dışına çıkaran soyutlama gücüdür.
Russell ve Whitehead: Mantığın Zirvesi

1910–1913 yılları arasında yayımlanan Principia Mathematica, matematiği yalnızca mantığın üzerine kurmayı amaçladı. Her önermenin saf mantıkla ispatlanabileceğini göstermek istediler. “1 + 1 = 2”nin bile yüzlerce sayfa sürmesi, bilginin temellerini ne kadar karmaşık hale getirebildiğimizi gösterdi. Her ne kadar bu proje tamamlanmamış olsa da, modern mantık biliminin doğuşunu sağladı.
Von Neumann: Kuantumun Dili

1932’de John von Neumann, Kuantum Mekaniğinin Matematiksel Temelleri adlı eserinde fiziğin karmaşık dünyasını matematikle yeniden tanımladı. Hilbert uzayları ve lineer operatörler aracılığıyla, rastlantısal görünen olaylara düzen getirdi. Bu, soyut matematiğin fiziğe uygulanabileceğinin en açık örneğiydi.
Grothendieck: Soyutluğun Zirvesi

- yüzyılın ortasında Alexander Grothendieck, Éléments de Géométrie Algébrique (EGA) adlı eseriyle cebirsel geometriyi tamamen yeniden inşa etti. “Şema teorisi” adlı kavramı tanıtarak sayı teorisi ile geometrinin birleştirilebileceğini gösterdi. Yüzyıllar önce Diophantus’un sorduğu bir soruya, Wiles’ın Fermat’nın Son Teoremi’ni ispatlamasında kullanılan dil onun soyut düşüncesinden doğdu.
Matematiği Öğretmek, Düşünmeyi Öğretmektir
Bu kitaplar, yalnızca birer tarihsel dönüm noktası değil, aynı zamanda birer eğitim manifestosudur. Her biri, bir çağın zihinsel sınırlarını genişletmiş, yeni bir düşünme biçimi öğretmiştir. Öklid düzeni, Arşimet sezgiyi, Cauchy titizliği, Cantor cesareti, Grothendieck ise hayal gücünü temsil eder.
Bugün bir öğrenciye matematik öğretirken, aslında bu fikirlerin yankılarını aktarıyoruz. Çünkü matematik, ezberlenen formüller değil, insan aklının evrimini belgeleyen bir düşünce tarihidir. Belki de asıl soru şudur: Bir gün, bizim çağımızdan da matematiğin seyrini değiştiren bir kitap çıkacak mı?



