Üslü Sayılarda Kavram Yanılgıları
Üslü sayılar, ortaokul matematiğinde gerçekten çok önemli bir konu. Hem ileride üst düzey matematik konularını anlamak için temel oluşturuyor hem de günlük hayatta karşılaştığımız büyüme, azalma ve ölçüm gibi birçok kavramı açıklıyor. Ama işin içine üslü sayılar girince öğrencilerin kafası bazen karışabiliyor ve bazı kavram yanılgıları ortaya çıkabiliyor.
Üslü sayıların ortaokuldaki önemi sadece işlem yapmayı öğrenmekle sınırlı değil; bu konu, çarpanlara ayırma, polinomlar, denklemler ve hatta veri bilimi gibi birçok matematiksel yapının temelini oluşturuyor. Eğer öğrenciler bu konuyu sağlam öğrenirse, lise matematiğinde de çok daha rahat ederler. O yüzden kavram yanılgılarını fark etmek ve bunları düzelterek ilerlemek oldukça önemli!
İçindekiler
Togglea^b=a.b Kavram Yanılgısı
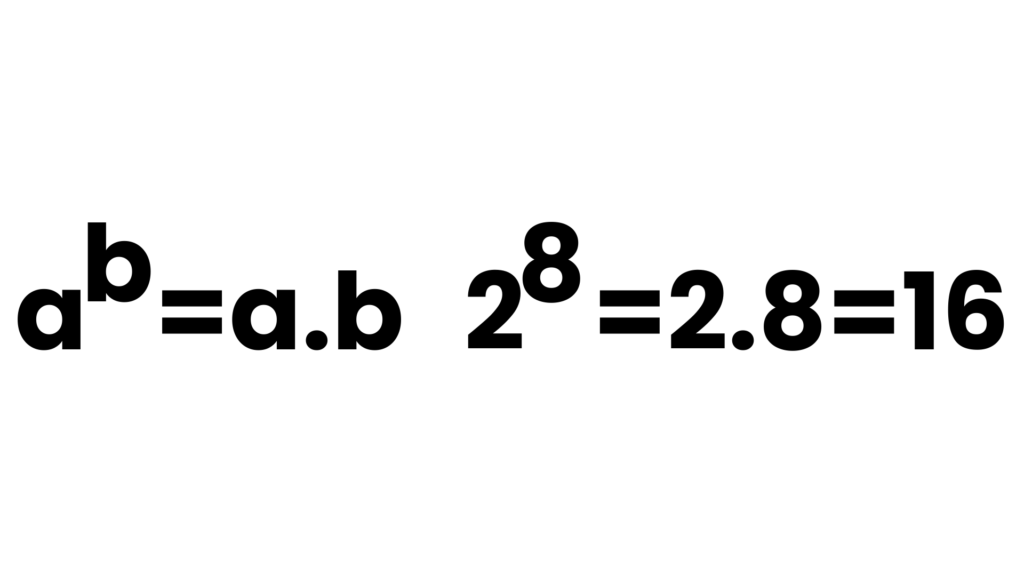
Öğrenciler üslü sayıların tanımını tam kavrayamadıkları için böyle bir yanılgıya düşmektedirler. Tanıma odaklanıp sonrasında bol bol örneklerle farklı gösterimler yaparak bu yanılgının önüne geçilebilir.
(-a)^b=-a^b Kavram Yanılgısı
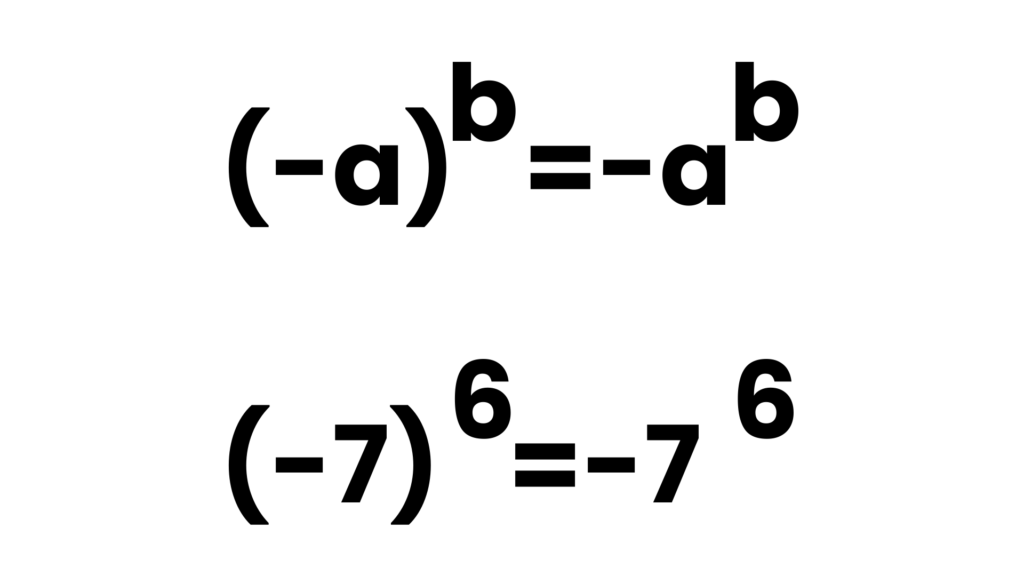
Bu yanılgının temel sebeplerinden biri öğrencilerin ‘bir rasyonel sayının karesinin daima pozitif olduğu’ bilgisini kullanarak yanlış sonuca ulaşmasıdır.
Bu iki ifadenin ne anlama geldiğinin öğrenci tarafından sözlü olarak açıklanmasının istenmesi öğrencinin kendi kendine iki ifadeyi ayırmasına yardımcı olabilir.
(−a)^b ifadesi n tane (-a)’ nın çarpılması gerektiğini anlatırken −a^b ifadesi n tane a’nın çarpımının negatifi anlamına gelmektedir. Üslü ifadeleri bu biçimde sözel hale dökmek bu sorunun ortadan kalkmasını sağlayabilir. Bunun yanı sıra ifadede a ve n yerine sayılara koyularak ifadenin sayısal olarak görülmesini sağlamak da bu güçlüğün giderilmesine yardımcı olabilir. Bu konuda öğrencilere hesap makinesinde üslü sayının değerinin nasıl hesaplanacağı gösterilip hesap makinesinden yararlanarak yaptıklarını kontrol etmeleri sağlanabilir.
a^b=b^a Kavram Yanılgısı
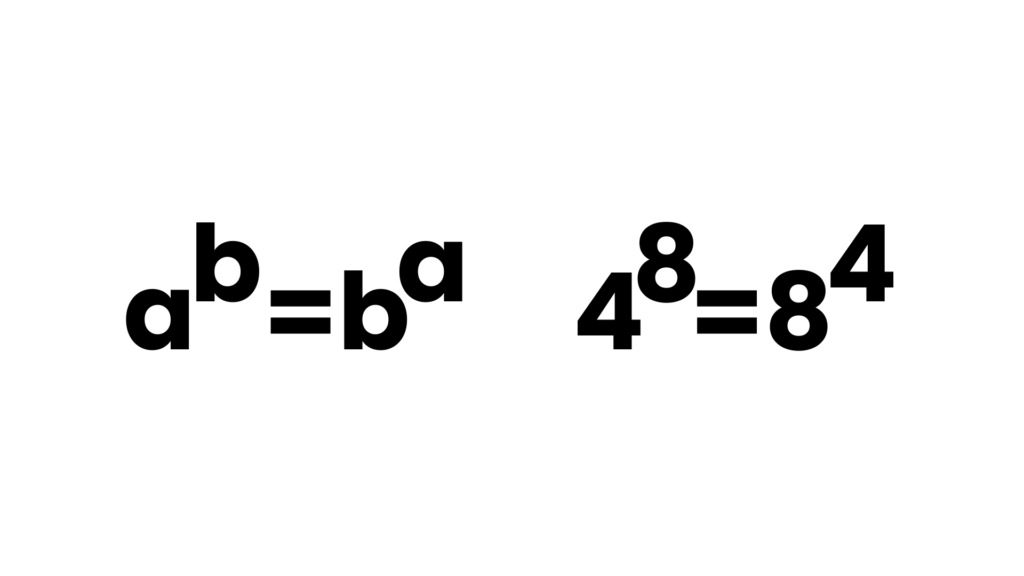
Öğrencilerin değişkenin kuvvetiyle bir sayının değişken olarak verilmiş bir kuvvetini yani, a gerçel bir değişken ve b bir doğal sayı olmak üzere a^b ve b^a ifadelerini birbirinden ayıramadıkları görülmüştür. Örneğin bazı öğrenciler x^2 ve 2^xifadelerinin her ikisinin de değerinin x^𝟐=𝟐^ax=𝟐x ya da x^𝟐=𝟐^ax=x.x olacağını düşünmüşlerdir.
Öğrencilerin bu güçlüğü yenmeleri için bu ifadelerin ne anlama geldiğinin sözlü olarak açıklanması ve ifadenin eşitinin yazılması istenebilir. Yani üslü sayının değerinin nasıl bulunduğunun hatırlanması sağlandıktan sonra, x^2→iki tane x’in çarpımı x^2=x.x 2x→x tane ikinin çarpımı 2^x=2.2.2…2 (x tane) biçiminde ifade edilmesi sağlanırsa öğrencilerin bu hataya düşme olasılıkları azalacaktır.
a^-b=-b^a Kavram Yanılgısı
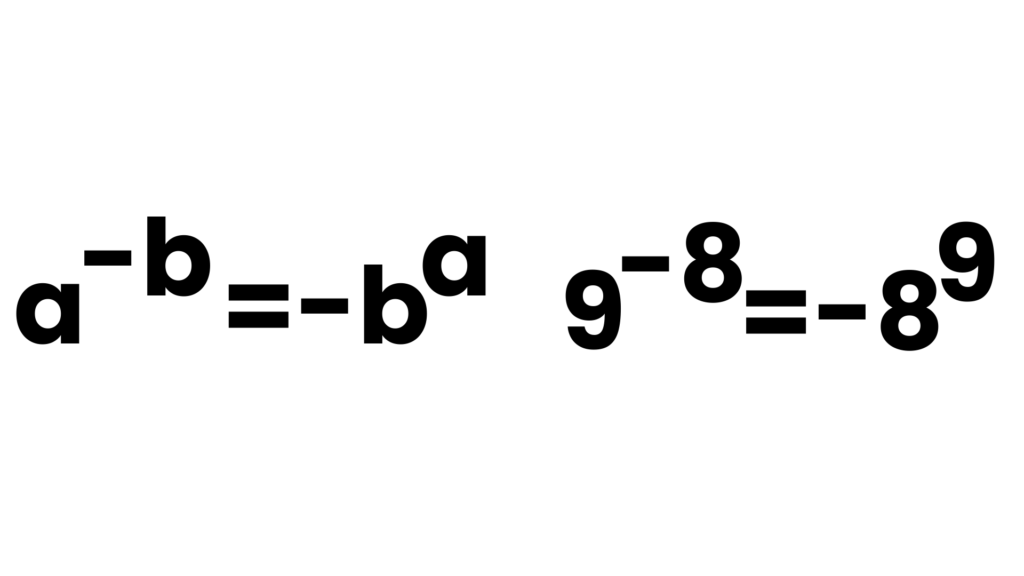
Yukarıdaki kavran yanılgısına benzer bir yanılgıdır. Temeli o yanılgıdır. Çoklu gösterimler üzerinde durulursa bu yanılgı önlenebilir.
a^b.c^b=(a.c)^(b+b) Kavram Yanılgısı
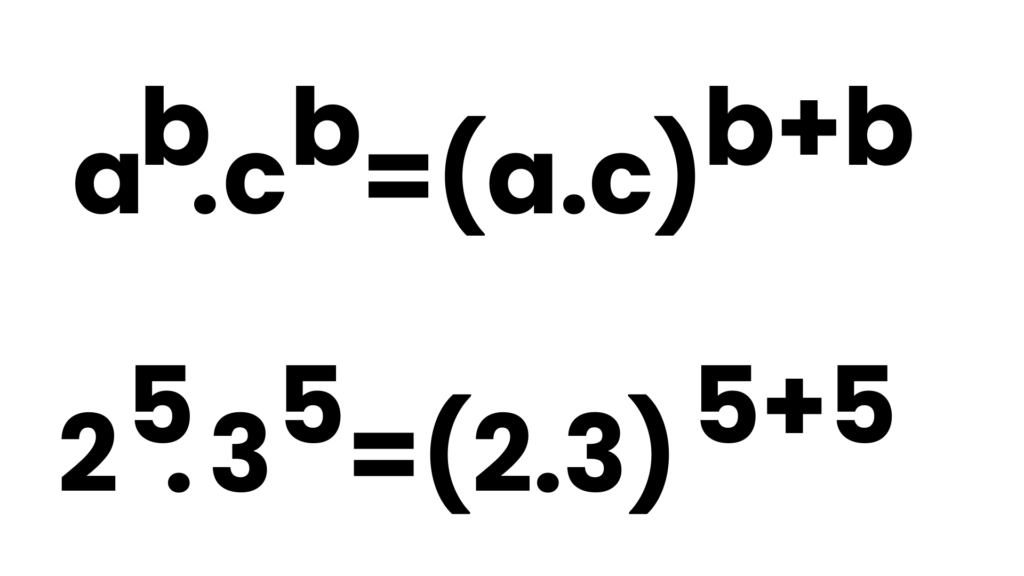
Öğrenci konu hakkında tam hakim olamadığından dolayı derste işlenilen iki farklı kuralı bir araya getirerek bir yanılgıya düşmüştür. Konu anlatım kısmına tekrar dönülmelidir.



